En el tema de hoy se analizara....
Recursividad
-Concepto
Recurrencia, recursión o recursividad es la forma en la cual se especifica un proceso basado en su propia definición. Siendo un poco más precisos, y para evitar el aparente círculo sin fin en esta definición:Un problema que pueda ser definido en función de su tamaño, sea este N, pueda ser dividido en instancias más pequeñas (< N) del mismo problema y se conozca la solución explícita a las instancias más simples, lo que se conoce como casos base, se puede aplicar inducción sobre las llamadas más pequeñas y suponer que estas quedan resueltas.
Para que se entienda mejor a continuación se exponen algunos ejemplos:
- Factorial(x: Entero): Sea N := x el tamaño del problema, podemos definir el problema de forma recurrente como x*Factorial(x - 1); como el tamaño de Factorial(x - 1) es menor que N podemos aplicar inducción por lo que disponemos del resultado. El caso base es el Factorial(0) que es 1.
- Ordenación por fusión(v: vector): Sea N := tamaño(v), podemos separar el vector en dos mitades. Estas dos mitades tienen tamaño N/2 por lo que por inducción podemos aplicar la ordenación en estos dos subproblemas. Una vez tenemos ambas mitades ordenadas simplemente debemos fusionarlas. El caso base es ordenar un vector de 0 elementos, que está trivialmente ordenado y no hay que hacer nada.
-Imagenes
Veremos algunas imagenes que demuestre que es recursividad
Imagen de cacao
Anuncio de cacao con una imagen recursiva. La mujer muestra un paquete idéntico al del propio anuncio, conteniendo así a otra mujer que muestra otro paquete más pequeño, de forma recursiva.
Triangulos repetidos
Imagen recursiva formada por un triángulo. Cada triángulo está compuesto de otros más pequeños, compuestos a su vez de la misma estructura recursiva.
Es amor es todo
Quien come a quien
Recursividad infinita
Quien mira a quien
-Aplicacion
Factorial -- n! = n × (n-1)!
-Para todo número natural n, se llama n factorial o factorial de n al producto de todos los naturales desde 1 hasta n:
A cada elemento de esta sucesión se le llama número de Fibonacci. Esta sucesión fue descrita en Europa por Leonardo de Pisa, matemático italiano del siglo XIII también conocido como Fibonacci. Tiene numerosas aplicaciones en ciencias de la computación, matemáticas y teoría de juegos. También aparece en configuraciones biológicas, como por ejemplo en las ramas de los árboles, en la disposición de las hojas en el tallo, en la flora de la alcachofa y en el arreglo de un cono.
-
En combinatoria, los números de Catalan forman una secuencia de números naturales que aparece en varios problemas de conteo que habitualmente son recursivos. Obtienen su nombre del matemático belga Eugène Charles Catalan (1814–1894).
El n-ésimo número de Catalan se obtiene, aplicando coeficientes binomiales, a partir de la siguiente fórmula:
- Las aplicaciones sucesivas de un operador binario pueden representarse con un árbol binario. En este caso, Cn es el número de árboles binarios de n + 1 hojas, en los que cada nodo tiene cero o dos hijos:
- Cn es el número de caminos monótonos que se pueden trazar a través de las líneas de una malla de n × n celdas cuadradas, de forma que nunca se cruce la diagonal. Un camino monótono es aquél que empieza en la esquina inferior izquierda y termina en la esquina superior derecha, y consiste únicamente en tramos que apuntan hacia arriba o hacia la derecha. El recuento de estos caminos es equivalente a contar palabras de Dyck: X significa "moverse a la derecha" e Y significa "moverse hacia arriba". Los siguientes diagramas muestran el caso n = 3:
Ahora bien, a efectos pedagógicos se puede utilizar una versión alternativa:
- Aqui le anexo un codigo en JAVA de programa de Fibonacci
/*-Videos
* To change this template, choose Tools | Templates
* and open the template in the editor.
*/
package fubonachi;
import java.util.*;
/**
*
* @author alumno
*/
public class Fubonachii
{
public int Fubonachii(int n, int fininf, int finsup)
{
Scanner Cap=new Scanner(System.in);
System.out.println("Ingrese un numero");
n=Cap.nextInt();
System.out.println("------------------------");
if(n==0||n==1)
{
System.out.println("La suma es " +n);
return n;
}
fininf=0;
finsup=1;
for(int i=2;i<=n;i++)
{
int x;
x=fininf;
fininf=finsup;
finsup=x+fininf;
System.out.println(" " +finsup);
}
return (finsup);
}
public static void main(String[] args)
{
Fubonachii fb= new Fubonachii();
int n=0, fininf=0, finsup=1;
fb.Fubonachii(n, fininf, finsup);
}
}
Torres de Hanoi
Teoria de Recursidad
Fuentes:
Texto
Videos
Imagenes







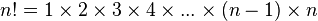













No hay comentarios:
Publicar un comentario