En computación y matemáticas un algoritmo de ordenamiento es un algoritmo que pone elementos de una lista o un vector en una secuencia dada por una relación de orden, es decir, el resultado de salida ha de ser una permutación —o reordenamiento— de la entrada que satisfaga la relación de orden dada. Las relaciones de orden más usadas son el orden numérico y el orden lexicográfico. Ordenamientos eficientes son importantes para optimizar el uso de otros algoritmos (como los de búsqueda y fusión) que requieren listas ordenadas para una ejecución rápida. También es útil para poner datos en forma canónica y para generar resultados legibles por humanos.
Desde los comienzos de la computación, el problema del ordenamiento ha atraído gran cantidad de investigación, tal vez debido a la complejidad de resolverlo eficientemente a pesar de su planteamiento simple y familiar. Por ejemplo, BubbleSort fue analizado desde 1956.1 Aunque muchos puedan considerarlo un problema resuelto, nuevos y útiles algoritmos de ordenamiento se siguen inventado hasta el día de hoy (por ejemplo, el ordenamiento de biblioteca se publicó por primera vez en el 2004). Los algoritmos de ordenamiento son comunes en las clases introductorias a la computación, donde la abundancia de algoritmos para el problema proporciona una gentil introducción a la variedad de conceptos núcleo de los algoritmos, como notación de O mayúscula, algoritmos divide y vencerás, estructuras de datos, análisis de los casos peor, mejor, y promedio, y límites inferiores.
Clasificación
Los algoritmos de ordenamiento se pueden clasificar de las siguientes maneras:- La más común es clasificar según el lugar donde se realice la ordenación
- Algoritmos de ordenamiento interno: en la memoria del ordenador.
- Algoritmos de ordenamiento externo: en un lugar externo como un disco duro.
- Por el tiempo que tardan en realizar la ordenación, dadas entradas ya ordenadas o inversamente ordenadas:
- Algoritmos de ordenación natural: Tarda lo mínimo posible cuando la entrada está ordenada.
- Algoritmos de ordenación no natural: Tarda lo mínimo posible cuando la entrada está inversamente ordenada.
- Por estabilidad: un ordenamiento estable mantiene el orden relativo que tenían originalmente los elementos con claves iguales. Por ejemplo, si una lista ordenada por fecha se reordena en orden alfabético con un algoritmo estable, todos los elementos cuya clave alfabética sea la misma quedarán en orden de fecha. Otro caso sería cuando no interesan las mayúsculas y minúsculas, pero se quiere que si una clave aBC estaba antes que AbC, en el resultado ambas claves aparezcan juntas y en el orden original: aBC, AbC. Cuando los elementos son indistinguibles (porque cada elemento se ordena por la clave completa) la estabilidad no interesa. Los algoritmos de ordenamiento que no son estables se pueden implementar para que sí lo sean. Una manera de hacer esto es modificar artificialmente la clave de ordenamiento de modo que la posición original en la lista participe del ordenamiento en caso de coincidencia.
- Complejidad computacional (peor caso, caso promedio y mejor caso) en términos de n, el tamaño de la lista o arreglo. Para esto se usa el concepto de orden de una función y se usa la notación O(n). El mejor comportamiento para ordenar (si no se aprovecha la estructura de las claves) es O(n log n). Los algoritmos más simples son cuadráticos, es decir O(n²). Los algoritmos que aprovechan la estructura de las claves de ordenamiento (p. ej. bucket sort) pueden ordenar en O(kn) donde k es el tamaño del espacio de claves. Como dicho tamaño es conocido a priori, se puede decir que estos algoritmos tienen un desempeño lineal, es decir O(n).
- Uso de memoria y otros recursos computacionales. También se usa la notación O(n).
Lista de algoritmos de ordenamiento
| Estables | ||||
| Nombre traducido | Nombre original | Complejidad | Memoria | Método |
| Ordenamiento de burbuja | Bubblesort | O(n²) | O(1) | Intercambio |
| Ordenamiento de burbuja bidireccional | Cocktail sort | O(n²) | O(1) | Intercambio |
| Ordenamiento por inserción | Insertion sort | O(n²) | O(1) | Inserción |
| Ordenamiento por casilleros | Bucket sort | O(n) | O(n) | No comparativo |
| Ordenamiento por cuentas | Counting sort | O(n+k) | O(n+k) | No comparativo |
| Ordenamiento por mezcla | Merge sort | O(n log n) | O(n) | Mezcla |
| Ordenamiento con árbol binario | Binary tree sort | O(n log n) | O(n) | Inserción |
| Pigeonhole sort | O(n+k) | O(k) | ||
| Ordenamiento Radix | Radix sort | O(nk) | O(n) | No comparativo |
| Distribution sort | O(n³) versión recursiva | O(n²) | ||
| Gnome sort | O(n²) | |||
-Burbuja
La Ordenación de burbuja (Bubble Sort en inglés) es un sencillo algoritmo de ordenamiento. Funciona revisando cada elemento de la lista que va a ser ordenada con el siguiente, intercambiándolos de posición si están en el orden equivocado. Es necesario revisar varias veces toda la lista hasta que no se necesiten más intercambios, lo cual significa que la lista está ordenada. Este algoritmo obtiene su nombre de la forma con la que suben por la lista los elementos durante los intercambios, como si fueran pequeñas "burbujas". También es conocido como el método del intercambio directo. Dado que solo usa comparaciones para operar elementos, se lo considera un algoritmo de comparación, siendo el más sencillo de implementar.
Análisis
Ejemplo del ordenamiento de burbuja ordenando una lista de números aleatorios.
Rendimiento del algoritmo
Al algoritmo de la burbuja, para ordenar un vector de n términos, tiene que realizar siempre el mismo número de comparaciones:
El numero de intercambios i(n), que hay que realizar depende del orden de los términos y podemos diferencia, el caso mejor, si el vector esta previamente ordenado, y el caso peor, si el vector esta ordenado en orden inverso.
Rendimiento en el caso desfavorable
Si pasamos al algoritmo un vector ordenado en orden inverso realizara un número de comparaciones:
Rendimiento en casos óptimos
En el caso optimo, el más favorable, es la ordenación que un vector ya ordenado, en este caso el número de comparaciones será el mismo que en cualquier otro caso:
Codigo
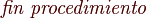
- -Quicksort
- Quicksort el ordenamiento rápido
El método de ordenamiento Quick Sort es actualmente el más eficiente y veloz de los métodos de ordenación interna.
Este método es una mejora sustancial del método de intercambio directo y recibe el nombre de Quick Sort por la velocidad con que ordena los elementos del arreglo. Su autor C.A. Hoare lo bautizó así.
es un algoritmo basado en la técnica de divide y vencerás, que permite, en promedio, ordenar n elementos en un tiempo proporcional a n log n.
El algoritmo original es recursivo, pero se utilizan versiones iterativas para mejorar su rendimiento (los algoritmos recursivos son en general más lentos que los iterativos, y consumen más recursos). Fue desarrollada por C. Antony R. Hoare en 1960.
Descripción del algoritmo
Elegir un elemento de la lista de elementos a ordenar, al que llamaremos pivote.La idea central de este algoritmo consiste en los siguiente:Se toma un elemento x de una posición cualquiera del arreglo.Se trata de ubicar a x en la posición correcta del arreglo, de tal forma que todos los elementos que se encuentran a su izquierda sean menores o iguales a x y todos los elementos que se encuentren a su derecha sean mayores o iguales a x.Se repiten los pasos anteriores pero ahora para los conjuntos de datos que se encuentran a la izquierda y a la derecha de la posición correcta de x en el arreglo.
Resituar los demás elementos de la lista a cada lado del pivote, de manera que a un lado queden todos los menores que él, y al otro los mayores. En este momento, el pivote ocupa exactamente el lugar que le corresponderá en la lista ordenada.
Repetir este proceso de forma recursiva para cada sublista mientras éstas contengan más de un elemento. Una vez terminado este proceso todos los elementos estarán ordenados.
Como se puede suponer, la eficiencia del algoritmo depende de la posición en la que termine el pivote elegido
Analisis del algoritmo:
Estabilidad: No es estable.
Requerimientos de Memoria: No requiere memoria adicional en su forma recursiva. En su forma iterativa la necesita para la pila.
Ventajas:Muy rápido.
No requiere memoria adicional.
Desventajas:Implementación un poco más complicada.
Recursividad (utiliza muchos recursos).
Mucha diferencia entre el peor y el mejor caso.
Ejemplo:
}El elemento divisor será el 6:
}5 - 3 - 7 - 6 - 2 - 1 - 4
} p
}Comparamos con el 5 por la izquierda y el 4 por la derecha con el pivote.
}5 - 3 - 7 - 6 - 2 - 1 - 4
}i p j
}5 es menor que 6 y 4 NO es mayor que 6. Avanzamos la i, y la j queda donde está.
}
}5 - 3 - 7 - 6 - 2 - 1 - 4
} i p j
}3 es menor que 6 y 4 NO es mayor que 6. Avanzamos la i, y la j queda donde está.
}
}5 - 3 - 7 - 6 - 2 - 1 - 4
} i p j
}7 NO es menor que 6 y 4 NO es mayor que 6.
}
}5 - 3 - 7 - 6 - 2 - 1 - 4
} i p j-ShellsoftEs un algoritmo de ordenamiento. El método se denomina Shell en honor de su inventor Donald Shell. Su implementación original, requiere O(n2) comparaciones e intercambios en el peor caso. Un cambio menor presentado en el libro de V. Pratt produce una implementación con un rendimiento de O(nlog2 n) en el peor caso. Esto es mejor que las O(n2) comparaciones requeridas por algoritmos simples pero peor que el óptimo O(n log n). Aunque es fácil desarrollar un sentido intuitivo de cómo funciona este algoritmo, es muy difícil analizar su tiempo de ejecución.
El Shell sort es una generalización del ordenamiento por inserción, teniendo en cuenta dos observaciones:
El ordenamiento por inserción es eficiente si la entrada está "casi ordenada".
El ordenamiento por inserción es ineficiente, en general, porque mueve los valores sólo una posición cada vez.
El algoritmo Shell sort mejora el ordenamiento por inserción comparando elementos separados por un espacio de varias posiciones. Esto permite que un elemento haga "pasos más grandes" hacia su posición esperada. Los pasos múltiples sobre los datos se hacen con tamaños de espacio cada vez más pequeños. El último paso del Shell sort es un simple ordenamiento por inserción, pero para entonces, ya está garantizado que los datos del vector están casi ordenados.
Implementacion:
public static void shellSort(int[] a) {
for ( int increment = a.length / 2;
increment > 0;
increment = (increment == 2 ? 1 : (int) Math.round(increment / 2.2))) {
for (int i = increment; i <>
for (int j = i; j >= increment && a[j - increment] > a[j]; j -= increment) {
int temp = a[j];
a[j] = a[j - increment];
a[j - increment] = temp;
}
}
}
}
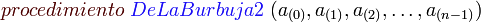
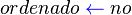
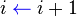
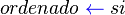
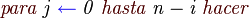
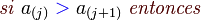
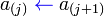
es un conjunto de pares no ordenados de elementos de 
.
.
es un conjunto de pares ordenados de elementos de 
es un conjunto de pares no ordenados de elementos de 
.
es un conjunto de pares ordenados y etiquetados de elementos de 
